When actually constructing a consensus phylogenetic tree such as the one shown at (Life on Earth) not only are a great many genetic traits taken into account, but a rigorous mathematical analysis of the actual DNA sequences of the organisms in question (where such DNA is available) is done to create cladograms (the branching diagrams showing patterns of descent) with the highest possible percentage confidence. These techniques have been tested in situations where the correct evolutionary relationships are already independently known for an absolute certainty to verify that they do in fact not simply produce an evolutionary relationship but the correct evolutionary relationship to within a very low margin of error..
One example:
http://mbe.oxfordjournals.org/cgi/reprint/19/2/170.pdf
In the paper above the researchers started with an original sample of DNA from Trypanosoma cruzi. They bred it over successive generations and allowed it to continually mutate, and every 70 generations 2 of the resulting DNA sequences were isolated at random and then used to found new populations. This process was repeated 4 times until 16 different ancestral DNA sequences had been generated. A rough diagram illustrating the process is shown in Figure 1 on page 2 of the paper.
Now this might not sound like much… but the number of possible phylogenetic trees that can be generated for a group of N different related genetic sequences increases in a steeply exponential manner as N increases. That number is described by the equation: (2N-3)!/((2^(N-2)) (N-2)!).
For 2 organisms this gives us only 1 possible tree (which should be obvious).
For 3 organisms it gives us 3 possible trees.
For 5 it gives us 105.
For 10 it gives us over 34 million.
For 16 organisms that gives us a total of (29!)/((2^14)(14!)) = 29!/1.428x10^15 = 6.19028x10^15 possible phylogenetic tree diagrams that can be generated. Picking the correct one isn’t something you can do by luck... unless of course you can beat better than 6 quintillion to 1 odds. And if that's the case, why aren't you in Vegas right now?
If you have mathematical routines that can, when applied to genetic sequences from those 16 organisms, subsequently generate the correct tree or even a very close approximation of it, it can safely be concluded that it’s because the routine works and works well.
So, they subjected the 16 final (terminal) sequences to phylogenetic analysis to see what the calculated highest likelihood phylogenetic tree for the organisms was. The result is displayed in figure 3 on page 5 of the paper. The top tree is the actual observed branching pattern during the experiment. Each of the circles represent a point at which sample sequences were isolated to found new populations… ie: an evolutionary branching of the population into two separate groups. They are numbered to correspond to the illustrated points in figure 1. The numbers along each branching line along the diagram represent the “branch length”. A value that can be used to represent either time between nodes… or amount of genetic sequence changes between nodes. In this case, the latter. For example, between node 2.1 and 3.1 the sequence undergoes 5 changes… while between node 2.1 and 3.2 it undergoes 6. T1 through T16 are the final 16 sequences generated as the end result of the process.
Displayed below that is the highest probability tree returned by the phylogenetic analysis of the sequences. Note that not only is every single node and branch correctly placed but the predicted length of each branch is also found in 29 out of 30 cases to within the calculated margin of error (on the branch linking the 2.2 and 3.3 nodes it missed the branch length by 1 sequence change more than it’s calculated margin of error.)
The entire evolutionary history of all 16 terminal sequences back to their common ancestor… reconstructed completely starting only from the end product and working backwards. Just as we can do with any other living things we have DNA samples from.
In short, the method works. Very well.
As noted in discussion of the previous topic there are, occasionally, some grey areas where it is not clear where a species should be placed in the tree to within a node or so due, in most cases, to some small scale discrepancy between phylogenies based on morphological data and phylogenies based on molecular or genetic data. An example will follow further down the post.
Evolution critics will often point to these regions of uncertainty as some kind of indication that evolutionary theory is incapable of explaining the evolutionary origins of some species… that evolution is “stumped” by certain species and should therefore be rejected. This is ludicrous. Even in a cladogram of only 16 organisms if this had been true of one of them… and a single branch had been mis-located by one node… given the amount of possible trees that had to be eliminated to arrive at the correct location for each of those nodes and branches it amounts to the equivalent of a margin of error in the results of 1 part in roughly 3x10^15…. or a measurement inaccuracy once we reach the equivalent of the 14th decimal place. An incredibly tiny margin of error if ever there was one.
To contrast … last I checked the charge of the electron has been measured reliably to 7 decimal places. G, the gravitational constant, to 3 decimal places. Nobody in their right mind suggests that this means we need to toss out physics and start from scratch because G and the charge of the electron “stumps” us through our inability to achieve a 100% perfect correlation between experimental results and theoretical modelling. 99.99% is pretty damn good too.
99.999999999...% is extraordinary. (They don’t say that evolutionary theory is one of the (if not the) most strongly evidentially supported scientific theories in the history of science just because they think it sounds good.)
Is it frustrating on those occasions when there is one branch on the tree with a positioning uncertainty of one branch... or maybe even two on sufficiently zoomed in scales? Yes. Ideally we would like to have absolutely every last detail right down to every single individual species nailed down with absolute certainty. It is why scientific research always continues to try to narrow those uncertainties... to add just that one more decimal place to that correlated value…
Is it somehow fatal to evolutionary theory that we still require some more data and better measurements to get that one branch position nailed down once and for all? Ridiculous.
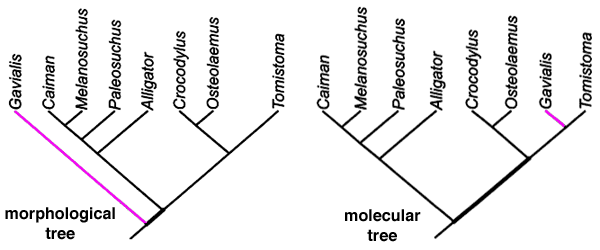
Actual example of discrepancy between two phylogenetic analyses:
These are two different phylogenies for species of crocodile. One based on the morphological data, one based on a molecular analysis of the c-myc proto-oncogene… taken from this study:
http://163.238.8.180/~fburbrink/Cour...s/gharials.pdf
Morhohological data will under almost any circumstances be considered secondary to molecular and genetic analysis... this being because the units of biological inheritance are the genes themselves. Analyzing morphology is observing a secondary characteristic of inheritance and thus has an expected slightly larger margin of error which can occasionally cause minor discrepancies in the two phylogenies like this one. If you scan down to the figure on page 8 of the linked paper you get a slightly better picture of the extent to which the sequences are analyzed to establish the tree in a genetic analysis. The chart shows the multiple mutations which were experienced along each branch to arrive at the final c-myc sequences.
The two charts created differ only on their placement of Gavialis. Based on the morphological data it was expected it would be less closely related to Tomistcoma than to other crocodiles… but the genetic analysis says they’re more closely related than other crocodiles. Notice that with the exception of the single Gavialis branch both trees are identical.
Note that even if we are to consider only these 8 species in isolation from the much larger tree into which they fit, and in which their position is well established, a difference of a single branch position for a single member of the group between one measurement and the other is minuscule. There are over one hundred and thirty five thousand possible phylogenetic trees for a group of 8 organisms… having the morphological and genetic sequence data correlate to this degree is an impressive level of agreement. Resolving that last branch position is the same as resolving a measurement out at the 4th or 5th decimal place.
No comments:
Post a Comment